Physical Problems in Neutron Star Mergers
Mergers of double neutron stars, or a neutron star and a stellar-mass black hole, have long been expected to occur in the universe with a rate being about three orders of magnitude lower than the supernova rate. Three major transient observable phenomena have been predicted to arise from a neutron star merger: (1) a gravitational wave (GW) signal, (2) a short gamma-ray burst (sGRB), and (3) a UV-optical-near-IR (UVOIR) transient powered by the radioactive decay of unstable heavy elements freshly synthesized in the merger ejecta. In addition, neutron star mergers have been proposed to be a major site for nucleosynthesis of heavy and rare elements (e.g., gold and platinum) in the universe.
In 1998 Paczyński and I investigated the electromagnetic radiation from a neutron star merger. We found that, decay of the unstable neutron-rich elements formed in the subrelativistic merger ejecta can power a transient event with the following characters: (1) The peak luminosity is in the supernova range and occurs at t ~1 day after the merger; (2) Near the luminosity peak the emissions are in the UV-optical band and characterized by blackbody radiations; (3) Both the luminosity and spectrum evolve rapidly with time, fading and reddening on a timescale of days (Li & Paczyński 1998, Astrophys. J., 507, L59). Later investigations indicated that the opacity arising from spectral lines of the lanthanide elements in the ejecta can be very high even if the abundance of lanthanides is very small, so that the resulting radiation is in the near-infrared band at t > 1 day (Kasen et al. 2013, Tanaka & Hotokezaka 2013). The transient is often named minisupernova, macronova, or kilonova in the literature.
On 2017 August 17, gravitational waves and electromagnetic radiations from a neutron star merger were discovered for the first time. About 10.48hr after the discovery of GW170817 by LIGO/Virgo and GRB170817A by Fermi/Integral, an optical counterpart SSS17a/AT2017gfo was identified in the field of GW170817/GRB170817A. The gravitational wave signal was consistent with being produced by binary stars with component masses between 0.86 and 2.26M⊙, in agreement with the masses of known neutron stars. Multiband observations of the optical source have identified brightness and spectrum features consistent with theoretical predictions for the optical transient from neutron star mergers. The early radiation of SSS17a/AT2017gfo has a thermal spectrum with the bulk energy in the UV-optical band. The bolometric luminosity of SSS17a/AT2017gfo derived from the observational data peaks at t ≈ 0.6 day and drops by a factor of ~ 3 from t = 1 to 3.5 day. The peak luminosity is ≈ 8×1041 erg s-1, in the range of faint supernovae (Waxman et al. 2018).
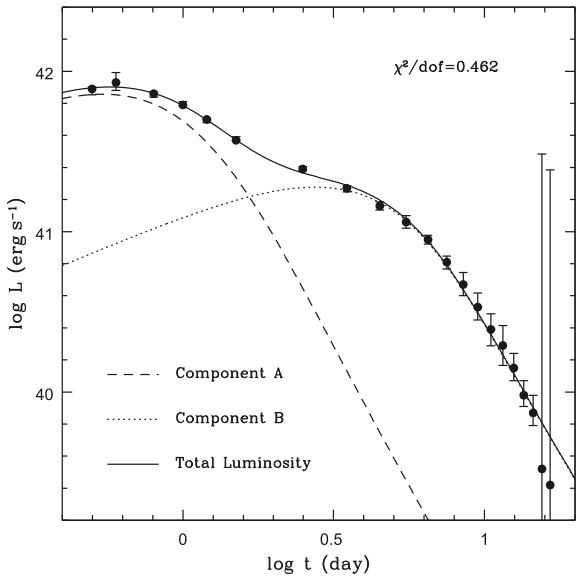
The above figure shows a best fit of the two-component Li-Paczyński model to the bolometric luminosity data of SSS17a/AT2017gfo (Li 2019, Astrophys. J., 872, 19). The excellent agreement between the model and the data confirms the neutron star merger origin for the optical source associated with GW170817/GRB170817A. Combined with the detection and interpretation of the gravitational wave, it makes the GW170817/GRB170817A a very solid case for the merger of two neutron stars.
In my opinions, there are three key physical problems in neutron star mergers that need be investigated urgently:
1. Nucleosynthesis in the merger ejecta. In principle the optical transient from a neutron star merger is powered by the radioactive decay of the unstable nuclei freshly synthesized in the merger ejecta through the rapid neutron-capture process (r-process). Hence, a precise knowledge about the species, abundance, and efficiency in converting mass to radiative energy of all the nuclei in the ejecta is crucial for an accurate calculation of the luminosity and spectrum of the optical transient as well as their evolution with time.
Accurate understanding of the nucleosynthesis in the merger ejecta is also important for predicting the spectrum of the radioactive gamma-ray emission after the ejecta becomes optically thin, and for understanding the formation of elements heavier than irons in the universe.
2. Opacity and radiative transfer in the merger ejecta. To evaluate the luminosity and spectrum of the optical transient correctly we need an accurate knowledge about the opacity and radiative transfer in the merger ejecta. Investigations have found that the opacity in the ejecta of a neutron star merger is very different from that in ordinary stellar matter (e.g., a supernova envelope). Due to the existence of a lot of heavy elements (especially lanthanides) and the fast expansion of the ejecta, the opacity arising from atomic spectral lines can be very high---for instance, several hundred times the opacity of electron scattering under appropriate conditions. Thermal radiation from an ejecta with such a high opacity would be in the near infrared band.
However, observations of SSS17a/AT2017gfo do not seem to support the above claim. At least in the early epoch (t < 1 day, for instance), the radiation is dominantly in the UV-optical band. The opacity derived from model fitting to the data is also not as high as that predicted for the opacity from spectral lines. Therefore, opacity and radiative transfer in the merger ejecta need more investigations.
3. Gravitational waves emitted by a neutron star merger. A system of double neutron stars (or, a neutron star and a black hole) is more complicated than a system of double black holes due to the fact that the former has more degrees of freedom (e.g., parameters specifying the equation of state of neutron matter). As a result, the gravitational wave emitted by a system of double neutron stars (or, a neutron star and a black hole) is expected to be more complicated than the gravitational wave emitted by a system of double black holes. It is important to identify the critical features that distinguish the gravitation wave emitted by a neutron star system from that emitted by a black hole system and can be applied to analysis of gravitational wave signals to quickly identify a neutron star system as the emitter.
Electrodynamics in Curved Spacetime
In general relativity, the gravitational field (or, equivalently, the spacetime) is described by the Einstein field equation. While for matter fields, an equation of physics in a flat spacetime is usually transplanted to a general curved spacetime by the "minimal substitution" rule, i.e., by replacing the Minkowski metric tensor ηab appearing in the equation by a general spacetime metric tensor gab and replacing the derivative operator ∂a associated with ηab by the derivative operator ∇a associated with gab. This is essentially reflection of the equivalence principle: At any point in a curved spacetime, it is possible to choose a local inertial frame so that within a sufficiently small region around that point laws of nature take the forms as in a flat Minkowski spacetime. The critical point is that the region must be sufficiently small (i.e., much smaller than the radius of the spacetime curvature) so that any term of matter coupled to the spacetime curvature can be ignored. So, with the minimal substitution rule, it is not possible to recover terms of matter coupled to the spacetime curvature, if those terms exist in the laws.
Applying the minimal substitution rule to the Maxwell equation in a flat spacetime, one gets an electromagnetic field equation in a curved spacetime
(1) ∇aFab = -4πJb ,
where the antisymmetric Maxwell tensor Fab is defined by the potential vector Aa through Fab=∇aAb-∇bAa, Ja is the electric current density vector. Equation (1) was originally proposed by Albert Einstein in 1916. Since then it was widely accepted as the standard generalization of the Maxwell equation in a curved spacetime and is often called the Einstein-Maxwell equation.The minimal substitution rule provides a simple and convenient machine for converting an equation of physics in a flat spacetime to an equation in a curved spacetime. Although it can guarantee that the derived equation in a curved spacetime satisfies the principle of general covariance and returns to the correct equation in a flat spacetime, the minimal substitution rule cannot guarantee that the equation derived with it must be correct in physics. For instance, if the correct field equation contains a term involving the spacetime curvature, the term is not present in a flat spacetime so cannot be recovered by the minimal substitution rule. Another problem with the minimal substitution is that if a field equation in a flat spacetime contains second or higher order derivatives of a vector or a tensor, the corresponding field equation in a curved spacetime derived by the rule is not unique. Since the order of derivatives of a vector and a tensor matters in a curved spacetime, the minimal substitution rule can lead to different field equations in a curved spacetime even starting from the same equation in a flat spacetime, if the order of derivatives is arranged in different ways.
The Maxwell equation contains second-order derivatives of the potential vector Aa. So, even if the "minimal substitution" rule is insisted, different electromagnetic field equations can be obtained in a curved spacetime. In fact, an electromagnetic field equation of the form
(2) ∇aFab - ξRbaAa = -4πJb
where Rab is the Ricci curvature of the spacetime and ξ is a number that can be of any value, can be derived from the minimal substitution rule and the Maxwell equation in a flat spacetime by appropriately arranging the order of derivatives of Aa. Since ξ is arbitrary, there are an infinite number of equations in a curved spacetime corresponding to the Maxwell equation in a flat spacetime. There are a number of reasons for proposing that equation (2) is a better candidate for the electromagnetic field equation in a curved spacetime than equation (1):1. The electromagnetic field equation (1) cannot describe a universe with a charge, but equation (2) can. In a homogeneous and isotropic universe with a uniformly distributed net charge, the electromagnetic field tensor must be vanishing everywhere otherwise the electromagnetic field would define a special direction. In such a universe equation (1) must be violated since the left-hand side is zero but the right-hand side is nonzero. For a closed universe with a nonzero net charge, the Einstein-Maxwell equation always fails regardless of the spacetime symmetry and the charge distribution. For a compact space of volume V, we can use a compact surface S to divide it into two parts: V1 and V2, with V = V1 + V2. We can apply the Gauss's law derived from equation (1) to V1 and V2 to evaluate the charge contained in each volume. Since V1 and V2 are enclosed by the same surface S with opposite directions, the charges in V1 and V2 derived from the Gauss's law have the same magnitude but opposite signs. Hence the total charge in the volume V must be zero.
The above two paradoxes indicate that the Einstein-Maxwell equation (1) need be modified to be applicable to the universe as a whole. Equation (2), as a modification to the Einstein-Maxwell equation, can describe a universe with a net charge without a problem. For instance, for a homogeneous and isotropic universe with a uniformly distributed net charge, because of the curvature-coupled term -ξRbaAa (which can be considered as an effective electric current density term) the left-hand side of equation (2) can be nonzero. The curvature-coupled term can also lead to a nonzero charge in a closed universe. (For detailed discussions on the above issues, see Li 2016, Gen. Relativ. Gravit., 48, 28.)
2. Equation (2) can be naturally derived from the Maxwell equation in a flat spacetime via the minimal substitution rule. Since ∂a∂bAa = (1+ξ)∂a∂bAa - ξ∂b∂aAa, where ξ is any number, ∂aFab = ∂a∂aAb - ∂a∂bAa can be substituted by ∇a∇aAb - (1 + ξ)∇a∇bAa + ξ∇b∇aAa = ∇aFab - ξ(∇a∇b - ∇b∇a)Aa = ∇aFab - ξRbaAa in a curved spacetime, according to the minimal substitution rule. Then equation (2) is obtained. Since ξ is arbitrary (ξ can even be a function), there are an infinite number of equations in a curved spacetime corresponding to the Maxwell equation in a flat spacetime. All these equations are consistent with the equivalence principle, since, in a region of size much smaller than the spacetime curvature radius, the curvature-coupled term in the equation is negligibly small for an electromagnetic field with a coherent spatial scale smaller than or comparable to the size of the region.
3. Equation (2) with ξ = -2 can be derived from the five-dimensional Einstein field equation, if our four-dimensional spacetime is a hypersurface in a five-dimensional bulk spacetime. By projection onto the hypersurface, the five-dimensional Einstein field equation is recast into: a four-dimensional tensor field equation, which can be interpreted as the gravitational field equation in a four-dimensional spacetime; a four-dimensional vector field equation, which in fact can be interpreted as an electromagnetic field equation in a four-dimensional spacetime; and a scalar constraint equation. The electromagnetic field equation derived this way has right the form of equation (2) with ξ = -2. (For details see Li 2016, Front. Phys., 11, 110402; Class. Quantum Grav., 33, 225008.)
Therefore, equation (2), which is parameterized by the parameter ξ and can be derived from the Lagrangian
(3) LEM = -¼FabFab - ½ξRabAaAb + 4π AaJa ,
is a natural generalization of the Einstein-Maxwell equation. Alternatively, the Einstein-Maxwell equation (1) can be regarded as a special case of the more general equation (2) with ξ = 0. What is the correct value of ξ? Is it 0, -2, or some other value? This question can only be answered by experiments and observations.
When the spacetime is Ricci-flat (Rab = 0, e.g., outside of a black hole or a star in a vacuum environment), the curvature-coupled term in equation (2) disappears. Hence, in a flat spacetime or in a curved but Ricci-flat spacetime, the new electromagnetic field equation (2) is identical to the Einstein-Maxwell equation. As a result, the curvature-coupled term in the new field equation has no effect on experiments under laboratory conditions. The new electromagnetic field equation (2) can only be tested in an environment where the effect of the Ricci curvature is large i.e. in an environment with a high mass density, e.g., inside a neutron star and in the early epoch of the universe. Application of the new field equation to such astrophysical systems deserves investigations, which may help to determine the value of ξ and whether we indeed live on a hypersurface in a five-dimensional spacetime.
Radiative Transfer in a Relativistic System
Relativistically expanding systems are often involved in violent explosion phenomena in astronomy, including gamma-ray bursts, neutron star mergers, and broad-line supernovae. For gamma-ray bursts, the ejecta generating the gamma-ray emission can have an expansion velocity so close to the speed of light that the corresponding Lorentz factor is ≳ 100. For neutron star mergers (neutron star-neutron star mergers and black hole-neutron star mergers), the expansion speed of the the associated ejecta can be ≳ 0.3 times the speed of light. For broad-line supernovae, the expansion velocity at the photosphere deduced from the observed spectral lines can be ≳ 0.1 times the speed of light. Investigation of the photon diffusion process and radiative transfer in a relativistically expanding system is very important for correctly understanding the energetic and radiative characters of the above mentioned violent explosion systems, e.g., for precisely predicting and interpreting the luminosity and spectrum and their evolution with time.
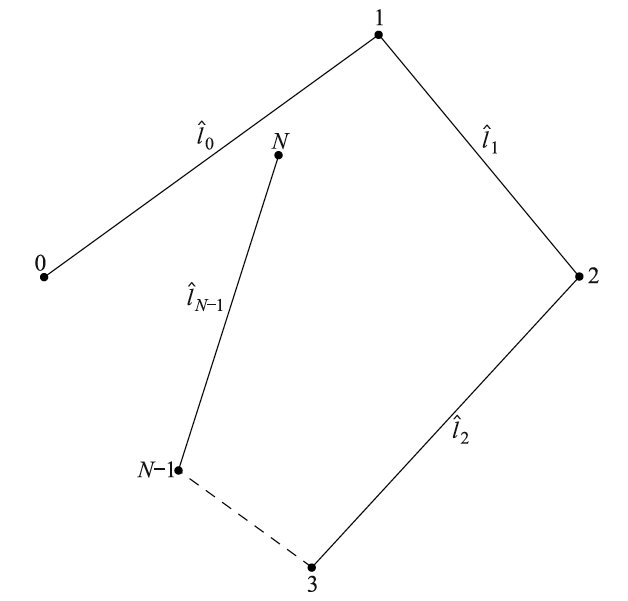
Random walks of photons are a key for understanding the photon diffusion and radiative transfer in a medium. The above figure shows random walks of a photon projected onto a spatial hypersurface of constant time in the comoving frame, Σ0 ≡ Σ(η = η0), starting from the moment η = η0 and point 0. The random walks can be caused by scattering with electrons, for instance. After a distance 0 (a proper spatial length on Σ0), the photon scatters at point 1 to a random direction along
1. After another distance
1, the photon scatters at point 2 to a random direction along
2, then scatters at point 3 ... After N steps of scattering, the photon reaches point N. From time η0 to time η, the total number of scattering during the whole process of random walks is derived to be
(4) N = ∫η0ηκ(η′)ρ(η′)cdη′,
where ρ(η′) is the mass density, κ(η′) is the opacity at time η′; and c is the speed of light. (For details see Li 2013, Front. Phys., 8, 555.)
Some of the research results are in principle also applicable to the universe, since the universe is also a relativistic expanding system.
Gamma-Ray Bursts and Supernovae
Since the launch of Swift on 20 November 2004, the research on gamma-ray bursts (GRBs) and their relation to supernovae has entered a completely new era. The fraction of GRBs (long and short) with measured redshifts and observed afterglows has increased rapidly. The association of (at least some) long GRBs with type Ibc supernovae has been laid on a solid foundation with the discovery of GRB060218 and the SN2006aj associated with it. However, despite the exciting progresses in observations, the nature of GRBs is still a great mystery and we do not have a standard model for GRBs yet. This gives us a large space for imagination and intellectual games.
Specific topics related to GRBs and supernovae that I am particularly interested in include:
The GRB-Supernova Connection In 2006, I found a remarkable correlation between the peak spectral energy of GRBs and the peak bolometric luminosity of the underlying supernovae, based on a sample of then available four pairs of GRBs and supernovae with spectroscopically confirmed connection. The relation may have important implications for the nature of the GRB-supernova connection.
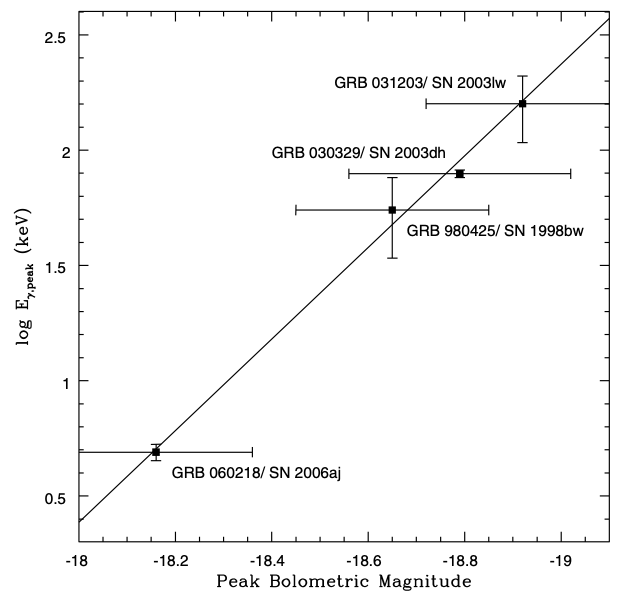
The above figure shows the peak spectral energy of GRBs versus the peak bolometric magnitude of the underlying supernovae for four pairs of GRBs and supernovae with connection. The straight line is a least-χ2 fit to the data: log Eγ,peak = -35.38 - 1.987 MSN,peak, where MSN,peak is the the peak bolometric magnitude of the supernova, Eγ,peak is the peak spectral energy of the GRB in keV. This relation is equivalent to
(5) Eγ,peak = 90.2keV (LSN,peak/1043erg s-1)4.97 ,
where LSN,peak is the peak bolometric luminosity of the supernova associated with the GRB. The physics for the relation is unclear yet. (For details see Li 2006, Mon. Not. R. Astron. Soc., 372, 1357.)
The relation (5) was later confirmed by the XRF080109 associated with a normal Type Ib SN2008D discovered in the spiral galaxy NGC2770 (Li 2008, Mon. Not. R. Astron. Soc., 388, 603).
GRBs and star formation Long GRBs occur in star forming regions and are thought to be produced by the core collapse of massive stars. Hence, people often assume that long GRBs trace star formation in the universe. However, some investigators have claimed that the rate of GRBs increases with cosmic redshift faster than the star formation rate (the figure below, where Q(z) is defined as an increasing function of redshift z), whose cause is not yet known.
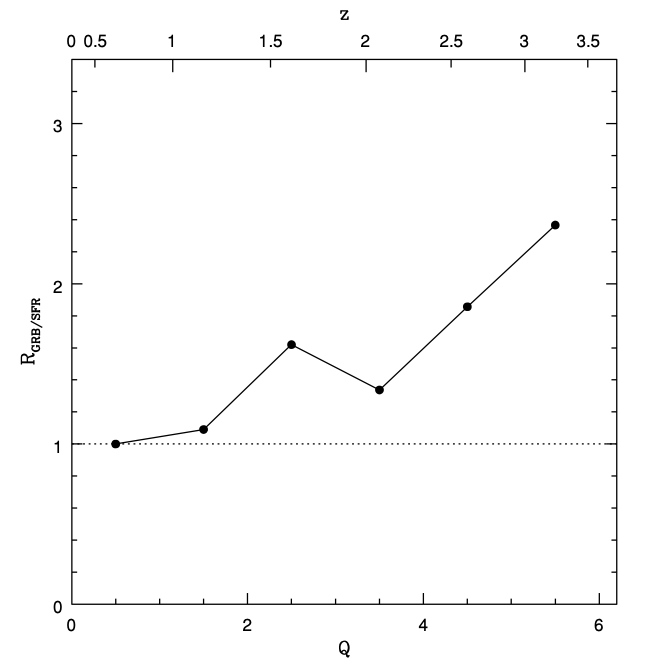
In 2008 I investigated the possibility of interpreting the observed discrepancy between the GRB rate history and the star formation rate history by considering the cosmic metallicity evolution. The motivation came from the observations that the cosmic metallicity evolves with redshift and GRBs tend to occur in low-metallicity galaxies. Adopting a simple model for the relation between GRB production and the cosmic metallicity history, I showed that the observed redshift distribution of the Swift GRBs can be reproduced with good accuracy. The results suggest that GRBs trace both star formation and metallicity evolution in the universe. If the star formation history can be accurately measured with other approaches, it will be possible to determine the cosmic metallicity evolution with the redshift distribution of GRBs. (For details see Li 2008, Mon. Not. R. Astron. Soc., 388, 1487.)
GRB Cosmology Various problems in GRBs as a tool (e.g., standard candle) to probe cosmology.
Black Holes and Accretion Disks
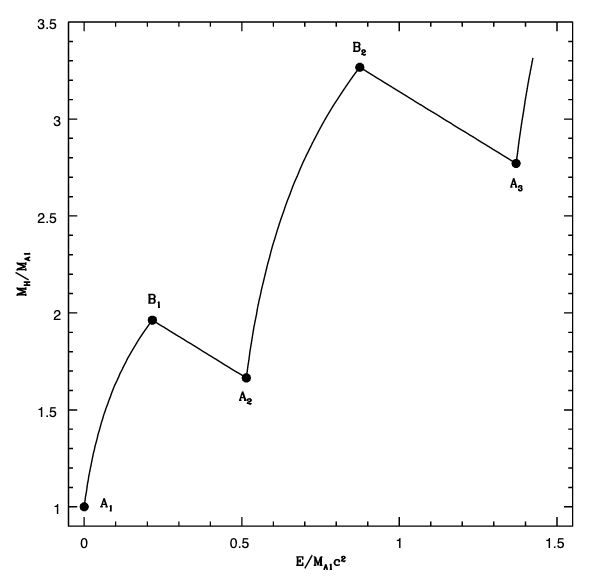
My Ph.D. thesis was on extraction of energy from black holes. In particular, I studied the magnetic interaction between a black hole and an accretion disk rotating around it, and extraction of energy from the black hole through the disk and the magnetic field. I found that a magnetic field bridging a black hole and an accretion disk plays an important role in the transportation of energy and angular momentum, and has an important effect on the spectrum of the energy radiated by the disk. When the black hole rotates faster than the disk, which can be attained for a Keplerian disk when the black hole spin a* > 0.36, the spin energy of the black hole provides an energy source for the radiation of the disk in addition to disk accretion. Such a disk has a radiation efficiency higher than that predicted by the standard theory (Li 2000, Astrophys. J., 533, L115; Li 2002, Astrophys. J., 567, 463). A new process was also discussed, in which periods of accretion from a thin disk, and the associated spin-up of the black hole, alternate with the periods of no accretion and magnetic transfer of energy from the black hole to the disk (see the figure below). These cycles can repeat indefinitely, at least in principle, with the black hole mass increasing by ~ 66% per cycle and up to ~ 43% of accreted rest mass radiated away by the disk. This is the highest efficiency of converting rest mass to energy by accreting into a black hole that has been ever proposed (Li & Paczyński 1998, Astrophys. J., 507, L59).
In collaboration with Ramesh Narayan et al., I have investigated the blackbody radiation spectrum from a thin Keplerian disk around a Kerr black hole and written a number of codes for accurately computing the spectrum. The codes have been compiled into a single subroutine: KERRBB, and installed into Xspec 12 — a standard X-ray data analysis package (Li et al. 2005, Astrophys. J. Suppl., 157, 335). Since then, KERRBB has been a standard tool for analyzing the spectra of X-ray binaries and estimating the spin of black holes. In a subsequent paper, we have extended the KERBB model to calculate the polarization of the blackbody radiation of a thin disk around a Kerr black hole. It has been found that observations of the polarized continuum radiation of the disk can used to infer the inclination of the disk and hence remove a degeneracy existing in determination of the parameters of an accretion system (Li, Narayan, & McClintock 2009, Astrophys. J., 691, 847).
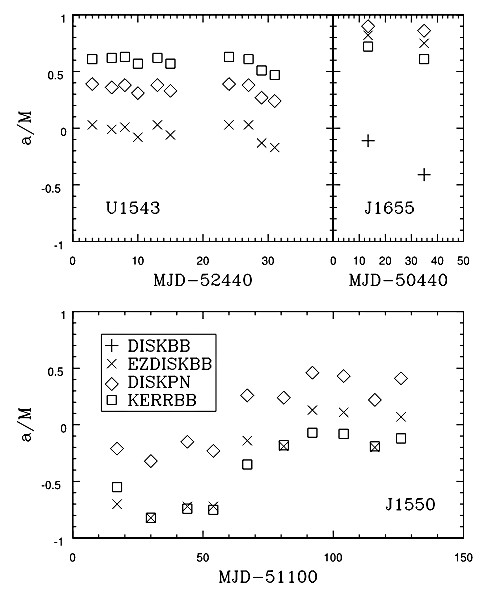
KERRBB is a powerful tool for measurement of the spin parameter of black holes in astronomy. In the above figure from Li et al. 2005, the spins of the black holes in three X-ray binary systems were estimated with four different disk models, but only the result of KERBB is trustable since only in this model the effect of general relativity is correctly included. Applying KERRBB to GRS1915+105, a very stringent lower limit on the spin of the black hole was obtained: a* > 0.98, close to the theoretical maximum rotation (McClintock et al. 2006, Astrophys. J., 652, 518). If the polarization data were available, we would be able to get more accurate estimates of the black hole spin because then we would have more accurate constraints on the disk inclination.
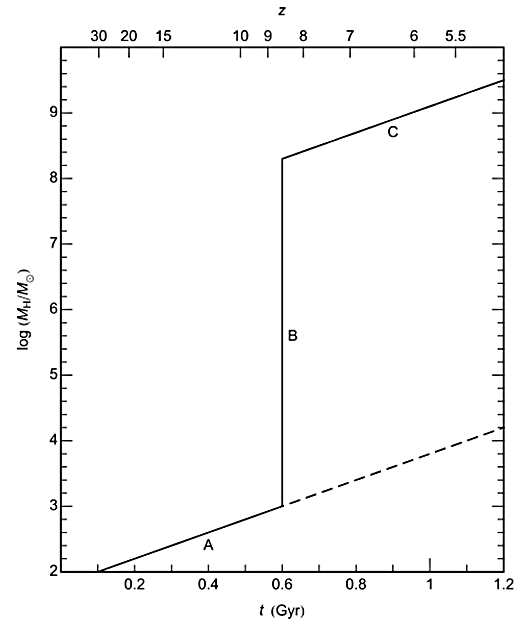
I am also interested in the physics of super-Eddington accretion and the growth of supermassive black holes at high redshifts. In 2012, I proposed that black holes in quasars have undergone a two-phase growing process: with a short super-Eddington accretion process they get their masses inflated by a very large factor until the feedback process becomes important, then with a prolonged sub-Eddington accretion process they have their masses increased by a factor of ≳ 2 (B and C in the figure below). The overall average efficiency of this two-phase process is ≳ 0.1, which is consistent with observational constraints. With this two-phase model the existence of black holes of masses ∼ 109 M⊙ at redshift ≳ 6 is easily explained (Li 2012, Mon. Not. R. Astron. Soc., 424, 146).
 Back to Li-Xin Li's Web Page
Back to Li-Xin Li's Web Page