Li-Xin Li

Spectral lines of heavy atomic elements in the ejecta of supernovae and neutron star mergers can have important contribution to the opacity of the ejecta matter even when the abundance of the elements is very small. Under favorable conditions, the line expansion opacity arising from spectral lines and the expansion of the medium can be orders of magnitude larger than the opacity of electron scattering. In a paper published in Astrophysical Journal in 2019, I derived the formulae for evaluating the line expansion opacity and its Rosseland mean in an expanding medium in the framework of special relativity, which can be considered as a generalization of previous work in the Newtonian approximation. Then I compared the derived relativistic formulae to the Newtonian ones to explore the relativistic effect on the opacity and test the new formulae with the spectral lines of some heavy atomic elements. I also derived some approximation formulae for the Rosseland mean of the line expansion opacity that are easy to use in numerical works while still maintaining a high-enough accuracy relative to exact solutions. The formulae derived in this paper are expected to have important applications in radiative problems related to relativistic astrophysical phenomena such as neutron star mergers, supernovae, and gamma-ray bursts where relativistic or subrelativistic expansions are involved.

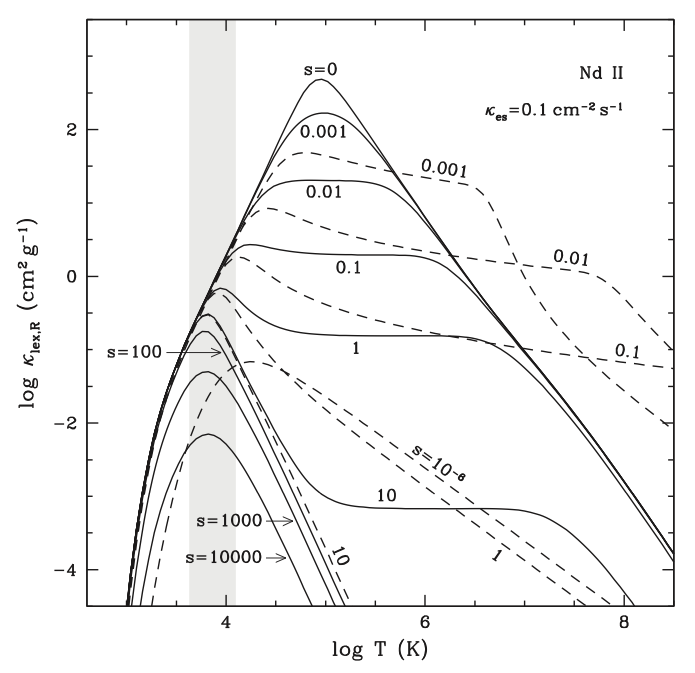
The above figure shows the Rosseland mean of the line expansion opacity as a function of temperature for various values of the expansion parameter s, calculated for Nd II with the relativistic formulae derived in my work (solid curves). For comparison, the results calculated with the Newtonian formulae derived by Karp et al. (1977) are shown with dashed curves. For s = 100, 1000, and 10,000, the results given by the Newtonian formulae are almost indistinguishable from that calculated with my relativistic formulae for the temperature range shown in the figure so they are not shown. The gray shaded region shows the location of spectral lines in the space of temperature, with the temperature of a line of frequency ν_l being defined by T_l = 0.261hν_l/k. [For details see L.-X. Li, Astrophys. J. 887, 60 (2019).]